Das Zahlenland – Mathematik spielerisch lernen im Vorschulalter

Gerhard Friedrich

 

 

 

 Inhalt

• Grundidee
• Zahlenweg
• Zahlenmärchen und Musik
• Zahlenhäuser und Zahlentürme
• Theoretischer Hintergrund
• Ergebnisse
• Akzeptanz im Alltag
• Resümee
• 5-Minuten-Spiele für zuhause

Grundidee

Das Konzept selbst basiert auf einer einfachen Grundidee, nämlich auf der denkbar konkretesten Interpretation des aus der Didaktik der Mathematik stammenden Begriffs „Zahlenraum“. Für die Zahlen von 1 bis 10 wurde nach einer geometrischen Systematik ein Ort geschaffen, in welchem die Zahlen „zu Hause sind“: das so genannte Zahlenland.

Dabei ist die Idee, die Zahlen bzw. umfassender, die Mathematik mit geometrischen Grundformen in Verbindung zu bringen nicht neu und bereits für den italienischen Physiker, Mathematiker und Astronom Galileo Galilei (1654-1642) war klar: „Das Buch der Natur ist mit mathematischen Symbolen geschrieben. Genauer: Die Natur spricht die Sprache der Mathematik: die Buchstaben dieser Sprache sind Dreiecke, Kreise und andere mathematische Figuren.“

 

 

 

 

 

 

 

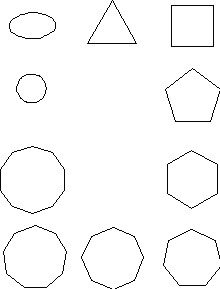
Schematischer Aufbau des Zahlenlandes

In diesem „Zahlenland“ erhält nun jede Zahl von 1 bis 10 einen festen „geometrisch dargestellten Wohnort“ (Kreis, Ellipse, Dreieck, Viereck, … , Zehneck, wir sprechen von „Zahlengärten“) und in Form eines Zahlentiers einen spezifischen Charakter bzw. eine unverwechselbare Identität.

Das Zahlenland entspricht dem fachdidaktischen Begriff des Zahlenraums. Im Zahlenland sind die Zahlen zu Hause, sie besitzen beseelte Eigenschaften und geben in personalisierter Weise ihre mathematischen Eigenschaften kund.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ausschnitt aus dem Zahlenland

Wesentliche Elemente des Zahlenlandes sind neben den bereits erwähnten Zahlengärten (geometrische Formen) und Zahlentieren vor allem der Zahlenweg, die Zahlenhäuser und –türme, besondere Zahlenmärchen und speziell für dieses Projekt komponierte Musik.

Zahlenweg

Dem Zahlenweg liegt eine entsprechend einfache Grundidee wie bei der Zahlenlandidee selbst zugrunde. Handelt es sich beim Zahlenland, wie bereits erwähnt, um eine anschauliche Interpretation des Zahlenraumbegriffs, so entspricht der Zahlenweg dem bekannten Zahlenstrahl, allerdings mit dem Vorteil, dass dieser im Raum mit dem ganzen Körper erkundet werden kann.

 

Kinder auf dem Zahlenweg

Zahlenmärchen und Musik

Zu jeder Zahl gibt es entsprechende Märchen mit mathematischen Inhalten. Eine Geschichte über die Eins erzählt etwa von der Eins und ihrem Einhorn. Die Geschichte der Zwei handelt davon, dass die Zwei sich darüber ärgert, weil die Menschen meinen, sie stottere, obwohl das gar nicht stimmt, denn „alle alle Zweien Zweien reden reden so so wie wie sie sie“ usw. Es gibt eine Drei, die drei Wünsche erfüllen kann usw.

Korrespondierend zu diesen Zahlengeschichten arbeiten wir mit Zahlenliedern, die streng „mathematisch“ komponiert wurden. So singt die „Eins“ ihr Lied mit nur einem einzigen Ton im Einertakt. Die „Zwei“ entsprechend mit zwei Tönen im 2/4 Takt, die „Drei“ liebt den Walzer und kommt mit genau drei Tönen aus usw.

Noten des Fünfer-Lieds im 5/4-Takt mit dem Tonumfang einer Quinte.

Zahlenhäuser und Zahlentürme

Die Zahlenhäuser und die Zahlentürme dienen als Einrichtungsgegenstände bei den Zahlengärten. Als Zahlenhäuser bezeichnen wir Holzwürfel, auf denen die Zahlen von ‚Eins’ bis ‚Fünf’ mit Hilfe einfacher Bohrungen abgebildet sind.
Diese Bohrungen, für die Kinder sind es Häuserfenster, lassen sich auf der Vorderseite mit Stöpseln verschließen. Die Fenster verkörpern damit den Anzahlaspekt der Zahlen. Ein herausnehmbares Fähnchen für die Ziffern lässt sich auf der Oberseite des Holzrahmens aufstecken. In der Idee des Zahlenlandes entsprechen die Ziffernfähnchen den Hausnummern.

Es bietet sich an, zu Beginn den Zahlenraum von 1 bis 5 zu thematisieren und anschließend als Basis zu benutzen, um den Zahlenraum bis 10 zu erweitern. Dies lässt sich dadurch erzielen, in dem wir den gesamten Zahlenraum von 1 bis 5, beginnend ab der 6, quasi nochmals verwenden. Den Zahlen, beginnend ab der 6, wird stets die Zahl 5, bzw. ein Haus der Zahl ‚Fünf’, beigestellt: 6=1+5; 7=2+5 bis 10=5+5.

Solche Zahlkombinationen lassen sich auch mit den Zahlentürmen darstellen. Bei den Zahlentürmen handelt es sich um farblich gekennzeichnete Holzwürfel, die mit Hilfe eines Holzzylinders aufeinander stapelbar und drehbar sind. Diese Zahlentürme bieten eine große Vielfalt an spielerischen Möglichkeiten der Zahlerkundung, insbesondere für das Thema Zahlzerlegung

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Zahlzerlegungen mit dem Zahlenlandturm

Theoretischer Hintergrund

Seine methodischen Ideen schöpft das Projekt aus verschiedenen Wissensbereichen:

• Der erste Bereich ist die „Neurodidaktik“. Ich benutze diesen Begriff als funktionalen Hilfsbegriff, um die Zusammenhänge zwischen den neurobiologischen Bedingungen des Menschen und seiner Lernfähigkeit zu beschreiben. Aus der Hirnforschung wissen wir beispielsweise, dass das Gedächtnis der Kinder in erster Linie durch konkrete Situationen und besondere Erlebnisse geprägt ist. Dies gilt insbesondere, wenn diese Erlebnisse oder Ereignisse einen Neuigkeitswert besitzen und den Kindern bedeutsam erscheinen. Aber Kinder können sich nicht nur die Ereignisse gut merken, sondern auch die Orte, an denen sie stattfanden. Beim Einspeichern einer Episode werden auch die zugehörigen Ortskoordinaten eingespeichert. Diesen beiden Tatsachen versuchen wir dadurch Rechnung zu tragen, indem jede Zahl einen festen Ort im Raum erhält und wir unsere Grundzahlen zu „Zahlereignissen“ werden lassen. Aus diesem Grund arbeiten wir neben vielgestaltigen Spielen vor allem mit Zahlenliedern und Zahlengeschichten mit dem Ziel, die Zahlen in episodische Handlungsabläufe einzubetten.
• Der zweite Bereich ist die Entwicklungspsychologie in Verbindung mit der Elementarpädagogik. Bei der Begegnung der Vorschulkinder mit der Welt der elementaren Mathematik bzw. der Zahlen arbeiten wir ganz bewusst mit so genannten “Anthropomorphismen” . Darunter versteht man ganz allgemein die Zuschreibung menschlicher Eigenschaften oder Verhaltensweisen auf nichtmenschliche Objekte oder auch Tiere. In unserem Konzept werden gezielt konstruierte Anthropomorphismen (in Form personalisierter Zahlen) als didaktische Hilfsmittel eingesetzt.
• Der dritte Bereich ist die Didaktik der elementaren Mathematik. Hier geht es vor allem darum, der Vielfalt verschiedener Zahlbedeutungen möglichst umfassend gerecht zu werden. In der Didaktik der Mathematik sprechen wir von Zahlaspekten, die im Zahlenlandkonzept Berücksichtigung erfahren.
• Neben den in der Mathematikdidaktik bekannten Zahlaspekten suchen wir darüber hinaus die Zahlen in musikalischen Strukturen und – vor allem – in der konkreten Lebenswelt der Kinder.

Ergebnisse

Es war unser Anspruch, wichtige Dimensionen des Projektes wissenschaftlich zu evaluieren. Dabei ging es uns vor allem darum nachzuweisen, dass die Kinder durch solch eine Art der Förderung in zentralen schulrelevanten Kompetenzen einen nachhaltigen Gewinn zu verzeichnen haben.

Dass solch ein Ansinnen nichts mit übertriebenem pädagogischen Ehrgeiz zu tun hat, wird dadurch untermauert, dass wir heute sehr genau wissen, dass die Anfänge des Zahlenverständnisses ebenso wie die des Lesen- und Schreibenlernens nicht erst mit dem systematischen Mathematik- bzw. Lese- und Schreibunterricht in der Grundschule beginnen, sondern weit in den Vorschulbereich hinein reichen. Dabei sprechen wir heute von so genannten schulischen Vorläuferfähigkeiten und meinen dabei insbesondere für den Bereich der Mathematik das mengen- und zahlenspezifische Vorwissen. Das sichere Beherrschen dieser Vorläuferkompetenzen, etwa die Fähigkeit zur Seriation (ein Element in eine vorgegebene Reihe einordnen), Mengenvergleiche (erkennen, dass die Anzahl einer Menge nicht durch die Anordnung der Elemente bestimmt wird), Zählfertigkeiten, einfache Rechenfertigkeiten mit konkretem Material und die Kenntnis der Zahlsymbole, ist eine wichtige Voraussetzung für die erfolgreiche Teilnahme am Mathematikunterricht in der ersten Klasse.

Und so ist es vielleicht auch nicht verwunderlich, dass die Ergebnisse unserer Studie sehr eindrucksvoll belegen, wie erfolgreich sich das Zahlenlandkonzept im Hinblick auf die Förderung mathematikspezifischer Lerninhalte erweist.

Akzeptanz im Alltag

Ein weiteres wichtiges Anliegen erschien uns neben der Untersuchung der Förderergebnisse die Beantwortung der Frage, inwieweit unser Konzept „alltagstauglich“ erscheint, d.h., inwieweit es auf breite Akzeptanz bei den Beteiligten stößt. Verfolgt man solch einen Anspruch ist es wichtig, das Konzept so zu entwerfen, dass es auf die didaktische Handlungskompetenz der Erzieherinnen und Erzieher zielt bzw. diese herausfordert. Ein Lernprogramm im Sinne einer lernpsychologischen Instruktionsanweisung oder eines Trainingsprogramms erschien uns nicht erstrebenswert. Uns war es wichtig, ein methodisches Rahmenkonzept maximalen Inhaltes so vorzugeben, dass es situativ an die soziokulturellen und individuellen Voraussetzungen und Bedingungen angepasst werden kann. Diese Anpassung und Konkretisierung kann jedoch nur der Pädagoge / die Pädagogin vor Ort leisten.

Aus diesem Grunde sollte das Konzept auch dafür offen sein, didaktische und methodische Ideen der Erzieherinnen und Erzieher aufzugreifen und umzusetzen. Um die Einstellung aller Beteiligten zum „Zahlenland“ zu erkunden, haben wir sowohl für die Erzieherinnen und Erzieher als auch für die Eltern der Projektkinder alle uns wichtig erscheinenden Aspekte in Fragen gekleidet. Die Antworten waren nahezu ausschließlich positiv.

Resümee

Das Zahlenlandkonzept wird inzwischen in sehr vielen Einrichtungen umgesetzt. Bei den Rückmeldungen die wir erhalten freut uns vor allem, dass wir neben Hinweisen, was jeweils aus unserem Konzept übernommen wurde auch erfahren, was konzeptionell verändert und im Hinblick auf die spezifische Einrichtung jeweils verbessert wurde. Dies ist auch völlig in unserem Sinne, da es uns, neben der Erhebung der wissenschaftlichen Daten in zentraler Weise darum geht, Erzieherinnen und Erzieher zu ermutigen, sich dem Thema der frühen mathematischen Bildung anzunehmen. Allen Antworten gemeinsam ist jedoch die Auskunft darüber, dass die Hauptpersonen, unsere Kinder also, sich mittels des Zahlenlandkonzeptes die Welt der Zahlen mit unglaublich großer Freude erschließen.

5-Minuten-Spiele für zuhause

Zu Schluss möchte ich noch verschiedene Spiele vorstellen, die alle kaum einen Vorbereitungsaufwand erfordern und die Sie leicht mit Ihrem Kind bzw. Ihren Kindern spielen können.

Nimm und Gewinn

Auf einem Tisch wird eine bestimmte Anzahl von Gegenständen (Murmeln, Nüsse, Cent-Stücke usw.) ausgeschüttet. Gewürfelt wird abwechselnd und man darf so viele Gegenstände wegnehmen, wie es Augen gewürfelt hat. Nachdem der letzte Gegenstand weggenommen wurde, wenden die gewonnenen Gegenstände verglichen. Wer am meisten besitzt, hat gewonnen.

Natürlich lässt sich dieses Spiel auch in umgekehrter Logik spielen. Jeder Spieler erhält einen gewissen Vorrat an Gegenständen (zum Beispiel 10, 12 oder 14). Entsprechend der gewürfelten Augenzahl darf er Gegenstände weglegen. Gewonnen hat derjenige, der als erstes alle Gegenstände losgeworden ist. Eine besondere Schwierigkeit kann man dadurch aufbauen, dass der letzte Wurf genau stimme muss.

Alles oder nichts

Zu Beginn wird eine gewisse Menge an Gegenständen (z.B. 20 Kastanien, Streichhölzer, Reißnägel etc.) halbiert und dann wird abwechselnd gewürfelt.
Die Augenzahl, die gewürfelt wird, darf dem Gegner weggenommen werden. Dann ist dieser an der Reihe. Das Spiel „purzelt“ auf diese Weise hin und her, bis entweder Sie oder ihr Kind keine Gegenstände mehr hat.

Eine besonders interessante und lehrreiche Variante besteht darin, mit echten Geldwerten zu spielen. Jeder Spieler erhält eine 5-Cent-Münze, zwei 2-Centmünzen und eine 1-Centmünze. Je nachdem welche Zahl gewürfelt wird, muss man die Geldbeträge dem Gegner geben.
Diese Erschwernis führt dazu, dass Spielzüge entstehen, bei denen „herausgegeben“ werden muss.

Greif hinein!

In einem kleinen Säckchen befinden sich kleine Kiesel- oder Muggelsteine. Ein Kind greift hinein und holt mit geschlossener Hand eine Anzahl an Steinen heraus. Nun muss es erraten bzw. erfühlen, wie viele es in der Hand hat. Natürlich dürfen weitere Kinder dabei mitraten. Das Spiel lässt sich auch variieren, indem z. B. eine Zahl vorgeben wird, die mit einem Griff als Anzahl der Steine herausgeholt werden muss.

Welche Zahl liegt unten?

Ihr Kind würfelt mit einem normalen Würfel. Nun muss das Kind sagen, welche Augenzahl es gewürfelt hat. Diese Augenzahl liegt natürlich „oben“ und die Antwort fällt einfach.

Wer weiß aber, welche Augenzahl unten liegt? (Die Summe aus gegenüberliegenden Augenzahlen ergibt stets 7.) Sicher können die Kinder diese Aufgaben nicht beim ersten Spielen beantworten, sie geraten aber immens ins Staunen, wenn ein Erwachsener die Antwort immer weiß und sind sie einmal hinter das Geheimnis gekommen, so haben sie größte Freude daran, das Ergebnis selbst „auszurechnen“ und es dann zu überprüfen.

Immer 10

Für dieses Spiel benötigen Sie so genannte Wendeplättchen. Wendeplättchen sind kreisrunde kleine Scheiben, deren eine Seite z. B. rot und die andere z. B. grün ist. Natürlich gehen auch anderen Farben, wichtig ist nur, dass sich die beiden Seiten farblich unterscheiden. Wendplättchen lassen sich leicht selbst herstellen, indem man z. B. 1-Cent Münzen beidseitig farbig überklebt oder indem man einen Korken in Scheiben zerschneidet und bunt anmalt. Aus dickerem Karton lassen sich diese natürlich auch sehr leicht herstellen.

Die Kinder werfen nun z. B. 10 Stück (jede andere Zahl geht natürlich ebenso) auf den Tisch und entdecken so ganz anschaulich die verschiedenen Zehnerzerlegungen, z.B. 4 rote und 6 grüne Plättchen.

Autor

PD Dr. Gerhard Friedrich, Dipl. Pädagoge, Jahrgang 1959 ist Lehrer für die Fächer Mathematik, Technik, Pädagogik und Psychologie; außerdem Mechaniker, Hobbymusiker und Vater von vier Kindern. Er beschäftigt sich seit 1990 mit Hirnforschung und Lernen, zunächst im Rahmen seiner Diplomarbeit in Pädagogik 1991, später in seiner 1995 abgeschlossenen Promotion in Erziehungswissenschaften. 2005 habilitierte an der Universität er in Bielefeld in Erziehungswissenschaften mit dem Schwerpunkt Schulpädagogik.

Literaturhinweise:

• Friedrich, G. u. Galgóczy, V. (2004). Komm mit ins Zahlenland. Eine spielerische Entdeckungsreise in die Welt der Mathematik. Freiburg: Christophorus.
• Friedrich, G. u. Galgóczy, V. (2004). Zahlenzwerge. Wer kann schon Zählen? Ein Lernspiel der Firma HABA-Spiele. Habermaaß: Bad Rodach.
• Friedrich, G., Galgóczy, V. u. Schindelhauer, B. (2006). Zahlenspiel und Zahlenspaß. Eine Praxismappe Mathematik für den Kindergarten und die Vorschule. Freiburg: Herder.
• Friedrich, G. u. Munz, H. (2006). Förderung schulischer Vorläuferfähigkeiten durch das didaktische Konzept „Komm mit ins Zahlenland“. In: Psychologie in Erziehung und Unterricht, 2006, 53 (S. 134-146).

Weitere Informationen

Erstellt am 19. Juli 2006, zuletzt geändert am 27. Oktober 2009